TFA Interview Guide for Quantitative Market Risk Management
- Pankaj Maheshwari
- Mar 24
- 24 min read
Updated: 7 days ago
What is Market Risk, and Why is it Important in Risk Management?
Market risk refers to the potential for financial losses due to unanticipated changes or fluctuations in the market risk factors, such as changes in interest rates, equity prices, foreign exchange rates, and commodity prices.
Equity Price Risk: The risk of losses due to changes in stock prices or indices. It is measured using Beta (ß), Volatility, and Value-at-Risk (VaR) models.
Interest Rate Risk: The risk of losses due to changes in interest rates, credit spreads impacting fixed-income portfolios. It is measured using sensitivities such as duration, convexity, and DV01, and can be managed via interest rate derivatives.
Foreign Exchange (Currency) Risk: The risk of losses due to changes in currency exchange rates. It is managed using currency hedging strategies such as forward contracts, options, and swaps.
Commodity Price Risk: The risk of losses due to changes in commodity prices (precious metals, agricultural products). It is managed using commodity futures and options.
Market risk is also known as systematic risk because it affects the entire financial system—it cannot be eliminated through diversification and affects all market participants. Unlike idiosyncratic risk (firm-specific risk), market risk arises from macroeconomic conditions, geopolitical events, monetary policy changes, and financial crises.
Importance in Financial Risk Management
Managing market risk is essential because it directly affects an institution's financial stability, profitability, and regulatory compliance. Below are key reasons why it plays a critical role in risk management:
Prevents Large Financial Losses: Market risk exposure can lead to substantial financial losses if not managed properly. Historical crises, such as the 2008 Global Financial Crisis, highlighted how exposure to market volatility (particularly in interest rates and credit spread) can affect even large institutions.
The collapse of Silicon Valley Bank (SVB) in 2023: SVB invested heavily in long-duration U.S. Treasury bonds and mortgage-backed securities during a period of low interest rates. However, as the Federal Reserve aggressively raised interest rates to combat inflation, the value of these fixed-income securities plummeted. SVB's risk management failed to adequately hedge this interest rate exposure. When the bank faced significant deposit withdrawals, it had to sell these securities at a loss, triggering a liquidity crisis. The losses eroded confidence, leading to a classic bank run and, ultimately, the bank’s collapse.
Ensures Regulatory Compliance: Financial institutions must adhere to risk management regulations, such as Basel III requires banks to maintain sufficient capital to cover market risk exposure, and IFRS 9 mandates financial institutions to measure and provision for changes in fair value driven by market movements, impacting financial statements.
The collapse of Lehman Brothers in 2008: Lehman had significant exposure to mortgage-backed securities (MBS) and collateralized debt obligations (CDOs), whose market values dropped sharply as the U.S. housing market worsened. These instruments became illiquid, and failure to accurately mark-to-market accounting and provisioning led to the extent of the losses. When asset prices dropped significantly and counterparties lost confidence, Lehman could not meet its obligations and filed for bankruptcy. This failure underscored the need for stricter capital requirements and fair value accounting standards, leading to reforms like Basel III and IFRS 9, ensuring banks now quantify and hold capital against such risks.
Enhances Financial Stability and Resilience: Institutions with strong market risk management practices are less prone to insolvency. It prevents excessive leveraging and speculation, and risk-taking by financial institutions.
What is Equity Price Risk, and How is it Measured in Market Risk Management?
Equity Price Risk refers to the potential for financial losses due to adverse movements in the prices of individual stocks or equity indices. It is a core market risk component and affects portfolios that hold equity exposures—whether through direct stock holdings, index derivatives, or structured equity-linked products.
Equity price risk is significant in market risk management because equity markets are inherently volatile, sensitive to macroeconomic indicators (GDP, inflation, interest rates), geopolitical events (trade war), earnings reports, and investor sentiment.
Key Metrics Used to Measure Equity Price Risk
Beta (β) – Systematic Risk Sensitivity: Beta measures the sensitivity of a stock’s return relative to the market (typically a benchmark index like the SnP 500). for example, a portfolio with a weighted Beta of 1.2 is expected to rise or fall 20% more than the market.
A Beta > 1 indicates higher volatility than the market (the stock is more volatile than the market).
A Beta < 1 indicates less volatility than the market (the stock is less volatile than the market).
It is used in the Capital Asset Pricing Model (CAPM) to estimate expected return. Risk managers use Beta to estimate how a stock or portfolio will perform under broad market movements, making it essential for factor-based risk decomposition and stress testing.
Volatility – Total Price Variability: Volatility is the statistical measure of the dispersion of returns for an asset, usually expressed as the standard deviation of historical returns. A higher volatility signals greater uncertainty and risk. for example, a stock with 30% annualized volatility suggests a one-standard deviation move of ±30% over a one-year period.
Historical volatility uses past market data.
Implied volatility (IV) reflects market expectations of future volatility, derived from option prices using models like Black-Scholes.
Volatility is used in VaR calculations, pricing derivative instruments, and to inform hedging strategies in portfolios with high volatility exposures in equities.
Value-at-Risk (VaR) – Potential Loss Estimation: VaR estimates the maximum expected loss on a portfolio at a given confidence level over a specified horizon. for example, a 1-day 99% VaR of $1 million suggests there's a 95% chance the loss won't exceed $1 million in a single day under normal market conditions. VaR does not quantify the size of losses beyond this threshold (that’s the role of Expected Shortfall).
VaR is central to risk-based capital allocation, regulatory reporting, and limit monitoring within equity trading desks and asset managers.
What are the Key Risk Metrics to Quantify and Manage Market Risk?
Market risk metrics are quantitative tools used by financial institutions to assess, monitor, and manage financial risk exposure to adverse price movements in financial markets. These metrics help to estimate potential losses, identify vulnerabilities, monitor risk limits, and implement risk mitigation strategies.
Value-at-Risk (VaR): It estimates the maximum potential loss in the value of a portfolio at a given confidence level (95% or 99%) over a specified time horizon (1 day or 10 days). VaR can be implemented through different methodologies, each offering distinct theoretical assumptions, computational requirements, and modeling precision suited to different portfolios, such as:
Historical Simulation Method: Also known as a non-parametric method.
Parametric (Variance-Covariance) Method: Also known as the analytical method or delta-normal method.
Monte Carlo Simulation Method
Expected Shortfall (ES or Conditional VaR): It estimates the average loss that would be incurred in the worst-case scenarios—specifically, those beyond the VaR threshold. It provides insights into the tail risk and, therefore, a more reliable measure for tail risk estimation compared to VaR.
Scenario Analysis and Stress Testing: These methods asses how a portfolio would perform (evaluate portfolio performance) under some specific historical (extreme market shocks) or hypothetical market conditions. for example, historical scenarios replicating actual crisis conditions: the 2000 Dot-Com Bubble, the 2008 Global Financial Crisis, the 1987 Black Monday Crash, and the COVID-19 Crash.
Sensitivity Analysis: It quantifies how the value of a portfolio or instrument changes in response to small movements in a specific market risk factor. It helps risk managers understand the first-order and higher-order exposures to facilitate portfolio risk decomposition, strategy formulation, risk attribution, and risk reporting. Risk sensitivities include Duration, DV01, Convexity, CS01, Delta, Gamma, and Vega.
Effective market risk management depends on the proper selection and interpretation of risk metrics. No single metric is sufficient; instead, a multi-metric framework ensures a more accurate, forward-looking, and resilient risk assessment process.
Explain Value-at-Risk (VaR) and Different Methods to Calculate VaR and Its Significance in Risk Management.
Value-at-Risk (VaR) is a statistical measure used to estimate the maximum potential loss in the value of a portfolio at a given confidence level (95% or 99%) over a specified time horizon (1 day or 10 days). It provides a single risk number that helps traders, risk managers, and financial institutions assess how much they can potentially lose under normal market conditions.
How Do You Interpret a 1-day 99% VaR of $10 million?
VaR answers the question: "What is the maximum loss a portfolio can face under normal market conditions over a given period, with a given probability?"
If a portfolio has a 1-day 99% VaR of $10 million, this means there is a 99% probability that losses will be less than or equal to $10 million with a 1% probability that the portfolio could lose more than $10 million in a single day. Read More
Different Methods to Calculate VaR
VaR can be implemented through different methodologies, each offering distinct theoretical assumptions, computational requirements, and modeling precision suited to different types of portfolios. The choice of method depends on the type of portfolio, the availability of data, and the desired level of accuracy.
Historical Simulation VaR: Also known as a non-parametric method, it uses actual historical returns/shocks to estimate potential future losses, avoiding any assumption a/bout the distribution of returns. It applies historical shocks in market risk factors to the current portfolio and derives the distribution of hypothetical portfolio returns. VaR is then determined by identifying the appropriate percentile based on the chosen confidence level. Read More
Parametric (Variance-Covariance) VaR: Also known as the analytical method or delta-normal method, it is based on the assumption that portfolio returns are normally distributed and that risk factors have a linear impact on portfolio value. It calculates VaR using a closed-form expression that incorporates the portfolio’s expected return, standard deviation, and a z-score corresponding to the selected confidence level. Read More
Monte Carlo Simulation VaR: It involves generating a large number of potential future scenarios by simulating the behavior of risk factors based on user-defined statistical distributions and correlation structures. Each scenario is applied to the portfolio to estimate potential changes to capture a wide range of outcomes. This method is well-suited for portfolios with complex or non-linear instruments, such as derivatives, and can model non-normal return distributions, fat tails, and volatility clustering.
In practice, risk managers often combine multiple approaches or use hybrid models to balance computational feasibility with accuracy and robustness.
Significance of VaR in Risk Management
VaR has become one of the most critical and widely used tools in the field of financial risk management. It provides a quantitative estimate of the potential loss in the value of a portfolio over a specified time horizon, at a given confidence level. Institutions use VaR not only for internal day-to-day market risk management but also to comply with regulatory mandates and make strategic capital allocation decisions.
Regulatory Compliance (Basel III, IFRS 9):
Basel III Framework: Under Basel III, banks are required (Internal Models Approach—IMA) to hold regulatory capital based on the amount of market risk they are exposed to. Although Basel III is progressively moving toward Expected Shortfall (ES) for measuring tail risk, VaR is still used widely for daily internal risk monitoring and reporting.
IFRS 9 – Financial Reporting Standards: In accounting standards, risk metrics VaR are used to model expected credit losses (ECL) for financial assets held at fair value. Institutions incorporate VaR and scenario analysis into probability-weighted loss forecasting.
Portfolio Risk Management: It helps traders, portfolio managers, and risk managers set risk limits (maximum allowable loss threshold) per asset class, and business, and allocate capital based on VaR estimates. VaR, Incremental and Marginal VaR, enables risk-adjusted performance analysis across trading strategies, funds, and businesses.
Scenario Analysis and Stress Testing: While VaR gives a snapshot under normal market conditions, it is also used as a starting point for more advanced and robust risk management techniques. Institutions apply historical or hypothetical stress scenarios to test the resilience of portfolios beyond the VaR threshold. These include the 2008 Global Financial Crisis, the 2020 COVID market shock, sharp interest rate hikes, and geopolitical disruptions.
The Basel III Fundamental Review of the Trading Book (FRTB) mandates Expected Shortfall (ES) for capturing tail risk. ES complements VaR by estimating the average loss in the worst 1% of cases, thus giving a comprehensive view of market risk exposure.
What are the Assumptions Behind the Historical Simulation VaR Method and Its Limitations in Calculating VaR?
Historical Simulation VaR is a non-parametric approach to estimating Value-at-Risk (VaR). Instead of assuming a specific distribution for asset returns, it relies on historical market data to assess potential losses.
It answers the question: "If past market movements were to repeat, what would be the worst-case loss over a given time horizon at a specified confidence level?"
Assumptions Behind Historical Simulation VaR
Past Market Behavior Reflects Future Risk: It assumes that historical price movements provide an accurate estimate of future risk, which means that if a particular market crash never occurred in the historical dataset, it won’t be reflected in the VaR estimate.
Returns Distribution Is Captured by Historical Data: Unlike parametric VaR, which assumes a normal distribution, Historical Simulation VaR relies entirely on the dataset of past returns. This removes the need for estimating volatility or correlations.
All Market Conditions Are Included in the Historical Dataset: The model assumes that the dataset includes a sufficient variety of market conditions (high volatility, low volatility, crises, etc.). If the dataset lacks extreme events, tail risks will be underestimated.
No Structural Changes in Market Dynamics: It assumes market behavior remains consistent and does not account for regime shifts (financial crises, major policy changes, and macroeconomic shocks). for example, a low-volatility period may underestimate risks, while a high-volatility period may overestimate.
No Model Estimation Errors: Since this approach does not use statistical estimation (like variance-covariance matrices), it assumes that the historical dataset is sufficient and unbiased.
Limitations of Historical Simulation VaR
It Fails to Capture "Black Swan" Events (Extreme Tail Risks): If an extreme event has never occurred in historical data, it is ignored in the risk estimation. for example, if a dataset covers only the past 3 years (a low-volatility period), the model will underestimate risk when a financial crisis occurs.
Solution: Use Expected Shortfall (ES) or incorporate stress testing to account for extreme risks.
Sensitive to the Chosen Time Window: Results depend heavily on the period selected for historical data. for example, if the dataset includes only post-crisis years (2010-2022), it may underestimate future risk because market volatility was low during that period.
Solution: Use Stressed VaR (SVaR) or incorporate regime-switching models to adjust for different market conditions.
Cannot Predict Future Market Conditions: Since Historical Simulation relies only on past data, it cannot anticipate new market dynamics (economic policy shifts, new asset correlations, changing liquidity). for example, if central banks introduce new monetary policies, Historical VaR will not adjust to these changes.
Solution: Use Scenario Analysis and Stress Testing, or combine historical analysis with Monte Carlo simulation for forward-looking risk assessment.
Limited Flexibility for Portfolio Risk Measurement: Historical VaR does not account for changing correlations between assets. for example, during a crisis, correlations between asset classes (stocks, bonds, commodities) tend to increase sharply, and Historical VaR may not capture these shifts.
Solution: Use stochastic correlation models or Monte Carlo methods to model dynamic risk.
Computationally Expensive for Large Portfolios: Requires storing and analyzing thousands of historical data points for every risk factor, making it computationally intensive for large institutional portfolios. for example, A hedge fund managing 500+ assets may require a large historical dataset, cashflow mapping, and risk mapping, making real-time risk calculations slow.
Solution: Optimize risk calculations using factor models or hybrid approaches. Read More
What are the Assumptions Behind the Parametric (Variance-Covariance) VaR Method and Its Limitations in Calculating VaR?
The Parametric VaR method, also known as the Variance-Covariance Approach or Delta-Normal VaR, is a statistical model that estimates risk based on the assumed normal distribution of returns. It calculates the potential loss of a portfolio using the mean and standard deviation (volatility) of asset returns, assuming that returns are normally distributed and independent.
Assumptions Behind the Parametric (Variance-Covariance) VaR Method
Asset Returns Follow a Normal Distribution: It assumes that asset returns are normally distributed, meaning no fat tails, skewness, or extreme events.
Limitation: Real-world returns often exhibit leptokurtosis (fat tails) and asymmetry, leading to the underestimation of extreme losses.
Constant Volatility (Homoskedasticity): It assumes that volatility remains stable over time.
Limitation: Volatility clustering occurs in real markets—volatility spikes during crises, making the model ineffective in stressed conditions. Solution: Use GARCH models to adjust for time-varying volatility.
Linear Relationships Between Assets (Stable Correlations): It assumes that asset correlations remain constant over time.
Limitation: During financial crises, correlations increase significantly (contagion effect). Solution: Use copula models or regime-switching models to account for changing correlations.
In 2008, assets that were previously uncorrelated became highly correlated, causing larger-than-expected losses.
Returns Are Independent Over Time: It assumes that yesterday’s return does not affect today’s return (no autocorrelation).
Limitation: Markets exhibit momentum and mean reversion, violating the independence assumption. Solution: Incorporate time-series models (ARMA, GARCH) to adjust for autocorrelation.
Portfolio Risk is Measured Using Variance and Covariance: Portfolio VaR is calculated using variance and covariance matrices of asset returns.
Limitation: This approach fails for portfolios with options or non-linear instruments, as options have convexity and Gamma risk. Solution: Use Delta-Gamma VaR (second-order Taylor expansion) for options portfolios.
Limitations of Parametric VaR
Underestimates Extreme Risk (Tail Risk): Since it assumes normally distributed returns, it fails to capture fat tails. for example, the 2008 financial crisis caused market drops far greater than what normal distribution predicts.
Solution: Use Expected Shortfall (ES) or Extreme Value Theory (EVT) to model tail risk.
Ignores Volatility Clustering (Ineffective in Crisis Periods): Volatility is not constant—markets exhibit volatility clustering, where large price moves follow other large moves. for example, during crises, markets become highly volatile, making Parametric VaR unreliable.
Solution: GARCH models can improve risk estimation by modeling time-varying volatility.
Fails for Non-Linear Portfolios (Options): The linear assumption does not hold for options, structured products, and convex instruments. for example, A portfolio containing options has non-linear payoffs due to Gamma risk, which Parametric VaR cannot capture.
Solution: Use Delta-Gamma VaR or Monte Carlo simulation for options portfolios.
Assumes Correlations Are Constant (Breaks in Stress Events): Historical correlations break down in extreme market conditions—assets that were uncorrelated become highly correlated. for example, Equities and bonds may have a negative correlation in normal times, but during market panics, both decline together.
Solution: Use stress testing and dynamic correlation models to improve accuracy.
Not Suitable for Fat-Tailed Markets: The normal distribution assumption fails for markets with frequent extreme events (emerging markets, commodities). for example, Oil prices can experience sudden crashes or spikes, violating normal distribution assumptions.
Solution: Use the Extreme Value Theory (EVT) or historical simulation for fat-tailed markets. Read More
What are the Assumptions Behind the Monte Carlo Simulation VaR Method and Its Limitations in Calculating VaR?
Monte Carlo Simulation VaR is a probabilistic risk estimation method that simulates multiple potential future market scenarios based on random sampling techniques. It models the distribution of potential losses by repeatedly generating thousands (or millions) of price paths for assets or portfolios.
Instead of relying on historical data (like Historical Simulation VaR) or assuming normality (like Parametric VaR), Monte Carlo Simulation allows greater flexibility in modeling non-linear instruments like options and structured products.
Assumptions Behind Monte Carlo VaR
Asset Returns Follow a Defined Probability Distribution: The Monte Carlo method requires an assumed probability distribution for asset price movements. Some underlying assumptions are: Geometric Brownian Motion (GBM) for stock prices, normal or lognormal distributions for returns, and fat-tailed or skewed distributions for risk-sensitive assets.
Limitation: The accuracy depends on choosing the correct distribution—if the model fails to capture market realities, the VaR estimate will be inaccurate.
Market Conditions Are Captured in the Simulated Scenarios: It assumes that simulated future price paths reflect realistic market movements based on volatility and correlation inputs. It allows flexibility to incorporate jumps, volatility clustering, and tail risks.
Limitation: If the simulation does not account for extreme events, it may underestimate tail risks.
Constant or Stochastic Volatility Assumption: Most basic models assume constant volatility over the simulation period. More advanced models incorporate stochastic volatility to reflect real-world volatility fluctuations.
Correlations Between Assets Are Stable: It assumes fixed correlation structures among portfolio assets. It uses historical correlation matrices for multi-asset portfolios.
Limitation: During stressed market conditions, correlations break down, making simulated results unreliable.
Large Number of Simulations Ensure Convergence: More simulations improve accuracy, but convergence depends on model quality. Typically, 100,000+ simulations are needed for stable estimates.
Limitation: Running a higher number of simulations can be computationally intensive, especially for complex derivatives portfolios.
Limitations of Monte Carlo VaR
Highly Dependent on Model Assumptions: If the wrong return distribution is fitted, Monte Carlo VaR will produce misleading risk estimates. for example, if the model assumes normal distribution, but actual returns have fat tails, it will underestimate risk in extreme events.
Solution: Use a distribution that accounts for fat tails, such as a t-distribution or a generalized Pareto distribution, to better capture extreme events.
Computationally Expensive for Large Portfolios: Monte Carlo requires thousands or millions of simulations, making it slower than Parametric or Historical VaR. for example, a portfolio with complex options, swaps, and multiple assets requires significant computing power.
Solution: Use variance reduction techniques like Antithetic Variates or Quasi-Monte Carlo methods to improve efficiency.
Correlation Instability in Crisis Events: Asset correlations are not stable- Monte Carlo assumes historical correlations hold, which fails in market crashes. for example, during the 2008 financial crisis, previously low-correlated assets became highly correlated, amplifying losses.
Requires Advanced Calibration for Non-Linear Instruments: For portfolios with option derivatives and exotic instruments, calibration of Gamma, Vega, and convexity risks is challenging.
Solution: Use Delta-Gamma Monte Carlo Simulation for better risk modeling of options portfolios.
Does Not Predict Extreme Events Unless Explicitly Modeled: If extreme tail risks are not included in the probability distribution, Monte Carlo fails to capture systemic risk. for example, the COVID-19 market shock was not predicted by standard models.
Solution: Combine Monte Carlo with Extreme Value Theory (EVT) to simulate rare events.
What are the Key Differences Between Historical, Parametric, and Monte Carlo VaR?
Value-at-Risk (VaR) is one of the most widely used risk management metrics for estimating potential portfolio losses. However, different methods exist for calculating VaR, each with its assumptions, advantages, and limitations, as we discussed in previous questions.
Differences Between VaR Methodologies
What are the Limitations of VaR, and How Does Expected Shortfall (ES) and Stressed Value-at-Risk (SVaR) Address Them?
VaR, though has some valid reasons for its popularity, especially within investment banks and other financial institutions, but it comes with a few limitations. Understanding these limitations is crucial for effective risk management, especially for complex portfolios and in periods of market stress. Read More
Dependence on Historical Data and Lookback Periods:
VaR calculations rely heavily on historical market data to estimate future risk. This introduces a key limitation: if the historical dataset does not include periods of extreme volatility or crisis, the VaR measure will likely underestimate potential losses.
The lookback period used (the number of past days or years considered) has a major impact on the accuracy of VaR. A short lookback period may reflect recent calm markets and fail to capture rare but impactful tail events, while an excessively long period may dilute the relevance of recent market conditions. for example, a VaR model using 2 years of calm market data (2017–2018) would miss the COVID-19 crash, giving a false sense of security in risk estimates.
Solution: Stressed Value-at-Risk (SVaR) is specifically designed to address the limitation of relying solely on benign historical periods in VaR calculations. It uses historical data from a period of significant financial stress (the 2008 Global Financial Crisis) to model potential losses under extreme but plausible conditions—ensuring that the risk measure captures tail events and periods of market dislocation that standard VaR might ignore.
VaR Does Not Capture Tail Risk (Fails in Extreme Events): VaR only provides the threshold loss at a given confidence level (95% or 99%), but it does not tell us the potential size of losses beyond this point. for example, if a portfolio has a 1-day 99% VaR of $10 million, this means there is a 1% probability of losing more than $10 million, but VaR does not quantify how much worse the losses could be.
In 2008 Global Financial Crisis, many institutions underestimated losses because VaR ignored extreme events.
VaR at 99% confidence does not account for the 1% worst-case scenarios, which is where catastrophic losses occur.
Solution: Expected Shortfall (ES) estimates the average loss beyond the VaR threshold (it measures the risk of extreme losses in the tail).
VaR Assumes Normal Distribution (Underestimates Fat-Tailed Risks): Parametric VaR assumes that asset returns are normally distributed, meaning it fails to capture fat tails (extreme price movements). for example, Stock market crashes exhibit leptokurtosis (fat tails), which means extreme losses occur more frequently than normal distribution predicts. VaR does not adjust for this and that makes risk estimates unreliable during financial crises.
The 2000 Dot-Com Crash, the 2008 Financial Crisis both saw extreme losses far beyond what normal distribution-based VaR predicted.
VaR Is Not Subadditive: A risk measure should satisfy subadditivity, which means that the risk of a diversified portfolio should not be greater than the sum of the individual risks. for example, suppose we calculate VaR separately for two different portfolios. When we combine them, the total portfolio VaR may be greater than the sum of the individual VaRs, violating subadditivity—making VaR unreliable for portfolio risk aggregation and capital allocation.
Solution: Expected Shortfall (ES) is sub-additive, meaning it accounts for diversification benefits and provides a more accurate measure of total risk.
VaR Is Highly Model-Dependent (Sensitive to Methodology): Different VaR calculation methods (Historical, Parametric, Monte Carlo) produce different results, making VaR highly dependent on the chosen model. Different banks report different VaR values for the same portfolio due to different modeling assumptions.
Parametric VaR (Variance-Covariance) assumes normality—underestimates risk in non-normal markets.
Historical VaR depends on past data and fails to predict future crises that haven’t happened before.
Monte Carlo VaR is more flexible but computationally expensive.
Solution: Expected Shortfall (ES) still depends on methodology, but it consistently captures extreme risks better than VaR, regardless of the method used.
When determining portfolio risk, a reliable risk measure is expected to incorporate correlations between each pair of assets. However, as the number of assets increases and the portfolio becomes more diverse across asset classes, sectors, and geographies, it becomes extremely challenging to estimate and maintain accurate correlations. Correlation matrices become unstable and noisy, especially when using limited historical data, leading to inaccurate aggregation of portfolio risk and ineffective diversification.
In large institutional portfolios with hundreds or thousands of positions, even small errors in estimating pairwise correlations can distort the overall risk profile, causing underestimation or overestimation of VaR.
What is Expected Shortfall (ES), and How Does it Differ from VaR?
Expected Shortfall (ES) (also known as Conditional Value-at-Risk (CVaR)) is a tail-risk measure that estimates the average loss in the worst-case scenarios, specifically beyond the Value-at-Risk (VaR) threshold at a given confidence level. for example, at a 97.5% confidence level, ES tells you the expected average loss in the worst 2.5% of cases.
It is considered a coherent risk measure, satisfying important mathematical properties that VaR does not (subadditivity), and is preferred in regulatory frameworks like Fundamental Review of the Trading Book (FRTB).
Key Differences Between Expected Shortfall and VaR
Measures Tail Risk vs. Threshold Loss:
VaR: Measures the maximum loss not to be exceeded at a given confidence level (say 99%). There is still a 1% chance the loss will exceed $10M.
ES: Measures the average loss if the loss exceeds the VaR threshold. If losses fall in the worst 1%, the average loss is $15M. ES provides more information about the severity of tail losses, while VaR provides only a cutoff point.
Sub-additivity and Coherent Risk Measures:
VaR is not always sub-additive, which means it may not respect diversification—the risk of a combined portfolio can be higher than the sum of individual risks.
ES is sub-additive, satisfying the requirements of a coherent risk measure, making it more reliable for portfolio-level risk aggregation.
Robustness in Fat-Tailed Distributions:
VaR may underestimate risk in markets with fat tails or skewness since it often assumes normality.
ES captures the full tail distribution and is more reliable in non-normal and crisis scenarios.
Regulatory Preference: Basel III now requires banks to use Expected Shortfall at 97.5% confidence for calculating capital under the FRTB (Fundamental Review of the Trading Book). This shift reflects the recognition that ES is a more accurate reflection of extreme market risk than VaR.
VaR is often misinterpreted as a worst-case loss, which it is not. ES clearly communicates the average loss in the worst-case scenarios, making it more intuitive for tail-risk-aware decision-making.
What are the Advantages and Limitations of Expected Shortfall (ES)?
Expected Shortfall (ES) (also known as Conditional Value-at-Risk (CVaR)) is a tail-risk measure that estimates the average loss in the worst-case scenarios, specifically beyond the Value-at-Risk (VaR) threshold at a given confidence level.
Advantages of Expected Shortfall (ES)
Captures Tail Risk More Effectively than VaR: ES quantifies not just the likelihood but the severity of losses beyond the VaR cutoff. It is essential for understanding the magnitude of extreme losses, especially in fat-tailed markets.
Satisfies Subadditivity – A Coherent Risk Measure: Unlike VaR, ES is subadditive, which means the risk of a diversified portfolio is never greater than the sum of its parts. This property ensures that diversification is properly rewarded, which makes ES suitable for portfolio-level risk aggregation.
Better for Regulatory Capital Calculations: Under Basel III/FRTB, ES has replaced VaR as the preferred risk measure for calculating market risk capital requirements. Regulators favor ES due to its greater sensitivity to tail risk and systemic shocks.
More Robust Across Different Distributions: It works well with non-normal return distributions, including those with skewness and fat tails. Unlike VaR, ES is less likely to underestimate risk when markets behave abnormally.
Suitable for Stress Testing and Scenario Analysis: ES is more aligned with real-world risk assessments, making it useful for stress testing, where extreme but plausible scenarios are considered.
Limitations of Expected Shortfall (ES)
Estimation Is Sensitive to Tail Modeling: ES focuses on the least frequent, most extreme observations in the distribution. This makes ES statistically unstable when the sample size is limited or if data lacks sufficient tail events. for example, in historical simulations, there may be very few observations beyond the VaR threshold, leading to inaccurate ES estimates.
Model Dependency in Parametric and Monte Carlo Approaches: In model-based approaches, ES is heavily influenced by assumptions about return distributions, volatility, and correlations. Incorrect model specifications can distort ES, just as they can with VaR.
Not As Intuitive to Communicate: ES provides an average loss, not a single cutoff like VaR, making it less intuitive for stakeholders unfamiliar with tail-based risk measures. It requires a deeper understanding of probability and risk concepts to interpret correctly.
Computationally Intensive for Large Portfolios: Especially in Monte Carlo simulations, ES requires evaluating and averaging all outcomes beyond the VaR threshold, which increases computational complexity.
Not Universally Adopted in All Risk Systems: Despite its regulatory backing, some legacy systems and risk models are still built around VaR, requiring significant infrastructure changes to adopt ES fully.
What are the Differences Between Scenario Analysis and Sensitivity Analysis?
In risk management, scenario analysis and sensitivity analysis are two risk metrics used to assess the impact of changes in market conditions on portfolio risk exposure. While they are often used together, they serve distinct purposes and are based on different approaches to stress testing and evaluating risk.
Sensitivity Analysis: It measures the change in the value of a portfolio or instrument due to a small change in a single risk factor while holding all other variables constant. It is used to understand how sensitive the portfolio is to each risk factor, such as interest rates, credit spreads, fx rates, equity prices, or volatilities. for example, a 1 basis point (0.01%) rise in interest rates' effect on a bond portfolio can be measured by DV01 or Duration, and a 1% increase in implied volatility and its effect on options' portfolios can be measured by Vega.
Scenario Analysis: It evaluates the impact of changes in multiple risk factors simultaneously, based on defined scenarios, which can be historical, hypothetical, or event-specific. It is used to simulate the effect of moderate (or extreme) but plausible market events (stress conditions) or macroeconomic shifts on a portfolio. for example, a scenario where interest rates rise by 100 bps, equity markets drop by 15%, and credit spreads widen by 50 bps, or a replay of the 2008 financial crisis or COVID-19 market shock.
Differences Between Sensitivity Analysis And Scenario Analysis
How do Option Sensitivities Help Manage Specific Risk Exposures in Options Portfolios?
Option Greeks are sensitivities that measure how an option's price changes in response to different factors, such as the price of the underlying asset, implied volatilities, time, and interest rates. These sensitivities provide critical insights into the risks associated with an options position (or an options portfolio) and allow traders and risk professionals to hedge their non-linear, multi-factor risk exposures effectively.
The most commonly used Option Greeks are:
Delta (Δ): It measures the rate of change of option price to changes in the underlying price.
Gamma (Γ): It measures the rate of change of option Delta to changes in the underlying price.
Vega (ν): It measures the rate of change of option price to changes in implied volatility.
Theta (θ): It measures the rate of change of option price to time decay.
Rho (ρ): It measures the rate of change of option price to changes in interest rates.
In sophisticated risk setups, especially involving exotic options, structured products, or large books, risk managers also consider Vanna, Volga, and Charm in risk management strategies.
Manage Directional Risk (Delta): Delta measures how much an option's price is expected to change for a $1 change in the underlying asset price. It is the first line of defense in managing directional exposure. It helps risk managers create delta-neutral positions, neutralize small price movements in the underlying (directional risk), thereby isolating other factors like implied volatility or time decay. A Delta-neutral position ensures that small price movements in the underlying do not impact the portfolio. for example, a trader short 100 calls with Delta = 0.50 per contract will have a total Delta of -50 (100 x -0.50). To neutralize this exposure, they can buy 50 shares of the underlying asset. Read More
Manage Convexity Risk (Gamma): Gamma measures how much the option's delta changes for a 1$ change in the underlying price, helping risk managers understand how Delta itself shifts by capturing the curvature of the PnL profile. High Gamma increases the risk of sudden large moves (delta shifts rapidly), especially at-the-money (ATM) options. for example, in a Delta-neutral but high-Gamma position, a small move in the underlying asset will require frequent adjustments to maintain the hedge—potentially increasing slippage and transaction costs.
Manage Volatility Risk (Vega): Vega measures how much an option's price changes for a 1% change in implied volatility (IV). Option traders use Vega-neutral strategies to isolate movements in the underlying without exposure to volatility shifts and time decay. It helps risk managers manage volatility risk, essential in event driven markets or earnings announcements or macroeconomic events. for example, a long straddle strategy has high Vega. If implied volatility drops significantly, the strategy could lose value even if the underlying remains near the strike price.
Manage Time Decay (Theta): Theta measures the rate at which an option loses value as time passes, assuming all else remains constant. Short options positions (for example, covered calls, short straddles) benefit from positive Theta, while long positions lose value. for example, an at-the-money (ATM) option has higher Theta decay as expiration approaches. A trader long on this option may need to adjust positions or close out early to avoid losses from time erosion.
Manage Interest Rate Risk (Rho): Rho measures how much an option's price changes for a 1% change in interest rates. While its impact is usually minor for short-dated options, it’s more relevant for long-dated options and interest rate-sensitive derivatives. Also, shifts in interest rates can alter the present value of expected payoffs, especially in structured or fixed-income-linked derivatives. for example, a trader managing a book of LEAPS (long-term equity options) or rate options must monitor Rho to adjust for macro shifts in the yield curve.
What is the Sensitivity-Based Partial Revaluation Approach, and Why is it Used in Risk Management?
The Sensitivity-Based Partial Revaluation approach is a widely used risk approximation technique that estimates how the value of an options or derivatives portfolio changes in response to small movements in market risk factors. It does so without performing a full revaluation (re-pricing each instrument using complex pricing models like Black-Scholes, binomial trees, or Monte Carlo simulations).
Instead of re-running full pricing models for every scenario or shock, the partial revaluation approach uses pre-calculated risk sensitivities, the Greeks (Delta, Gamma, Vega, etc.), to approximate portfolio-level or instrument-level value changes.
The sensi-based partial revaluation approach is based on a Taylor series expansion of the option's value function, truncated at first or second order. The commonly used Delta-Gamma-Vega (DGV) approximation incorporates three primary risk sensitivities:
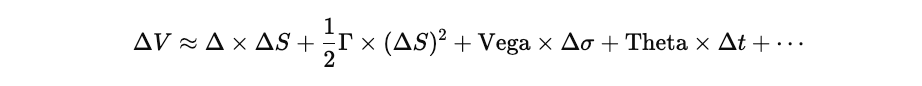
Higher-order Greeks (Volga, Vanna, Vomma, Charm, etc.) may be included for more precision, especially in portfolios with exotic derivatives, but the DGV approximation often provides sufficient accuracy for risk estimation and decision-making.
Why is it used in Risk Management?
Computational Efficiency: In large institutions, portfolios may consist of thousands of options and structured products. Running full revaluation models on every instrument/trade consumes time and computational resources and may be impractical for day-to-day risk management or real-time risk monitoring. Instead, the sensi-based partial revaluation approach uses precomputed sensitivities to quickly estimate how portfolio value changes with movements in underlying factors, allowing for fast re-calculation of PnL and risk exposure.
Practical Hedging and Risk Management Insights: Sensi-based partial revaluation doesn’t just save time, it breaks down where the risks lie. By decomposing the risk / portfolio’s exposure into first-order and second0-order components, the sensi-based approach provides actionable insights into the sources of risk and how to monitor, mitigate, and manage risk exposures effectively:
Delta: Underlying Price → Directional (Linear) Risk → Hedge Using Underlying Asset or Futures.
Delta tells the immediate exposure to price changes and lets traders and risk managers hedge directionally using simple linear instruments.
Gamma: Underlying Price → Directional (Convexity) Risk → Monitor Delta Shifts.
Gamma warns that the Delta hedge will go stale quickly, alerting traders and risk managers to be proactive in volatile markets.
Vega: Implied Volatility → Volatility Risk → Hedge Using Long/Short Vega Instruments.
Vega shows how vulnerable the portfolio is to changes in market uncertainty, which is critical in earnings season, macro events, or stress regimes.
This enables targeted hedging decisions, for example, whether to adjust linear (Delta) or non-linear (Gamma) risk exposure, reduce Vega risk exposure, or reduce non-linear (Gamma) risk in high-volatility environments.
Foundation for Regulatory Capital Models: Under the Basel III enhancements known as the Fundamental Review of the Trading Book (FRTB), regulators now allow, require banks to use sensitivity-based approaches under the Standardized Approach (SA).
These sensitivities are aggregated across risk classes (equity, FX, interest rate, credit, commodities).
Instead of requiring model-specific revaluations, the regulator prescribes risk weights and correlation parameters for sensitivities, thereby reducing dependency on complex full valuation models.
留言