The Mathematical Foundations of the Vasicek Model for Interest Rate Dynamics

The Vasicek model, introduced by Oldřich Vasicek in 1977, marked a significant milestone in the evolution of interest rate modeling. As one of the earliest mean-reverting stochastic models, it represented a fundamental shift from the random walk frameworks that had previously dominated financial theory. By capturing both the tendency of interest rates to revert to a long-term mean and the influence of random market shocks, the Vasicek model established a more realistic and theoretically sound foundation for modeling term structure dynamics.

At the heart of the model lies a stochastic differential equation (SDE) that governs the evolution of interest rates over time:

Where:

• 𝑟𝑡 is the interest rate at time 𝑡,

• 𝛼 is the speed of mean reversion (how quickly the interest rate reverts to the mean),

• 𝜇 is the long-term mean level of the interest rate,

• σ is the volatility of interest rate changes,

• 𝑊𝑡​ is a Wiener process representing the random shocks affecting the rate.

Mean Reversion

One of the most distinctive and valuable properties of the Vasicek model is its mean-reverting nature. Unlike models such as Geometric Brownian Motion (GBM)—where variables can drift indefinitely—the Vasicek model assumes that interest rates fluctuate around a central, long-term equilibrium level.

The term 𝛼(𝜇−𝑟𝑡) is central to this behavior. It ensures that the further the interest rate deviates from its long-term mean 𝜇, the stronger the pullback towards it. The parameter 𝛼, often referred to as the mean reversion speed, plays a crucial role in determining how quickly the interest rate reverts to mean 𝜇:

• A higher 𝛼 results in a faster reversion to the mean.

• A lower 𝛼 leads to a slower adjustment (gradual approach), allowing interest rates to remain away from the mean for extended periods.

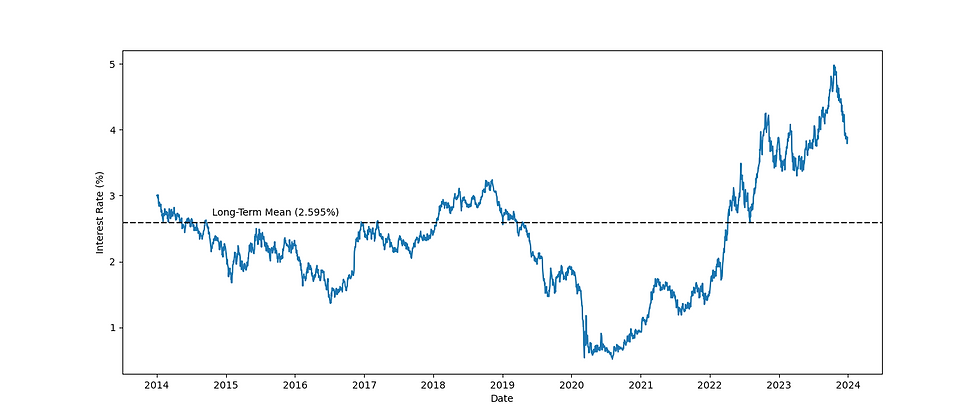
This reflects the empirical observation that interest rates tend to revert to a stable level over time, a phenomenon frequently supported by historical data. It also makes the model particularly appealing in fixed-income analysis, where mean-reversion aligns well with the observed behavior of short-term interest rates.

Why Is Mean Reversion Important?

Mean reversion is more than a mathematical convenience—it reflects the policy actions of central banks and monetary authorities. These institutions routinely intervene in markets to manage inflation, control economic growth, and stabilize financial systems. Through interest rate adjustments (interest rate hikes/cuts), they push rates toward targeted levels.

In the context of bond pricing and interest rate derivatives, mean reversion allows for capturing more realistic behavior and accurate valuation by constraining the path of future interest rate projections. Without this property, models can produce unrealistic outcomes such as indefinitely rising or negative interest rates, which are inconsistent with macroeconomic fundamentals and monetary policy frameworks.

Volatility and Random Shocks

The second component of the Vasicek model is the volatility σ and the random shocks introduced by the Wiener process 𝑑𝑊𝑡 that captures the unpredictable fluctuations (randomness) inherent in financial markets that cause the interest rate to deviate from its mean-reversion level.

The term 𝜎.𝑑𝑊𝑡 represents the differential of a weiner process—a mathematical representation of Brownian motion—that introduces stochastic volatility into the model. This component allows the model to account for inherent randomness and unpredictable fluctuations in interest rates due to market forces, investor sentiment, macroeconomic announcements, and other exogenous shocks.

How Does Volatility Influence the Model?

The parameter σ represents the standard deviation of interest rate changes, and it plays a crucial role in shaping the behavior of the model:

• A high σ value introduces greater randomness, allowing the rate to deviate significantly further from its mean, which increases the degree of uncertainty in future interest rate paths.

• A low σ value implies more stability, with the rate closely tracking its mean-reverting trajectory.

An important simplifying assumption in the Vasicek model is that volatility is set constant over time. This implies that the degree of randomness in interest rate movements remains unchanged, regardless of current market levels or conditions. While this assumption allows for analytical simplicity and easier calibration as the stochastic component behaves uniformly across time, it does limit the model’s flexibility in capturing volatility clustering or regime changes, which are common in real-world interest rate data.

Moreover, as the time increment Δ𝑡 becomes smaller, the approximation to the continuous-time Vasicek process improves, and the constant volatility assumption becomes more defensible (aligning the model's performance more closely with the underlying theoretical continuous process). However, with larger time steps Δ𝑡 or in volatile environments, the constant volatility assumption may overlook potential fluctuations in market volatility, leading to underestimation or overestimation of risk, depending on the prevailing market dynamics.

The Vasicek model elegantly combines mean-reversion with stochastic volatility to offer a theoretically robust and practically applicable framework for modeling interest rate behavior. Its development laid the groundwork for more advanced models and remains a cornerstone in the field of quantitative finance and interest rate risk management.

Subsequent sections in this series will further explore the model's empirical calibration, backtesting results, stress-testing capabilities, and comparisons with more flexible stochastic frameworks.