Understanding Gamma and Its Role in Options Trading and Risk Management
- Pankaj Maheshwari
- Jun 29, 2022
- 6 min read
Updated: Nov 27, 2024
Gamma is a second-order derivative metric in options trading, measuring the rate of change in an option's delta with respect to changes in the underlying asset's price. While delta reflects an option's sensitivity to price changes, gamma quantifies how delta itself changes, offering deeper insights into the non-linear nature of options pricing.
Gamma is a fundamental sensitivity measure in options pricing, quantifying how an options delta changes in response to a $1 movement in the underlying asset's price. As options delta, Gamma plays a critical role in both trading and risk management, offering deeper insights into potential price movements and directional risk.
Definition 1: Gamma measures the rate at which an option's delta changes in response to price changes in the underlying asset, assuming all other factors remain constant.
Definition 2: Gamma is an amount by which the option's delta is expected to change with respect to a $1 change in the underlying asset's price, keeping other factors constant.
As per the definitions,
Option Gamma = Δ Option Delta / Δ Underlying Price

Practical Example:
this example is in continuation to Understanding Delta and Its Role in Options Trading and Risk Management
Consider the following 1-Day price movements:
Strike Price is $1490.00
Underlying Price changes from $1488.05 to $1498.05
Call Option Delta changes from $0.4785 to $0.6435
Put Option Delta changes from $-0.5215 to $-0.3565
Therefore, using the sensitivity approach,
Call Option Gamma = (CDt - CDt-1) / (St - St-1) = (0.6435 - 0.4785) / (1498.05 - 1488.05) = 0.0165 represents that the call option's delta is expected to change by $0.0165 for every $1 change in the price of an underlying asset.
Put Option Gamma = (PDt - PDt-1) / (St - St-1) = (-0.3565 - -0.5215) / ( 1498.05 - 1488.05) = 0.0165 represents that the put option's delta is expected to change by -$0.0165 for every $1 change in the price of an underlying asset.
Option's gamma is a second-order derivative i.e. a derivative (gamma) of a derivative (delta) as it measures the rate of change of an option's delta stating how fast an option changes its directional movement. The important point to note here is that an option's gamma i.e. the rate of change of the option's delta of calls and puts is exactly equal.
"gamma influences the delta of calls and puts in the same direction"
In our example, the price of the underlying asset increases by $10.00 from $1488.05 to $1498.05 and so the call option's delta as well from $0.4785 to $0.6435 reflects a higher probability and higher expected payoff in case the option expires in the money. The change of $0.0165 is getting added to the call option's delta. However, the put option's delta decreases from $-0.5215 to $-0.3565 reflecting a lower probability of the option expiring in the money. Again, the change of $0.0165 is getting added to the put option's delta.
Irrespective of calls or puts, the option's gamma will remain equal as the impact on the option's delta of both calls and puts is equal as highlighted above in the example.
"gamma is always positive for long and negative for short"
In our example, if the price of the underlying asset decreases by $10.00 from $1488.05 to $1478.05, the call option's delta will also decrease from $0.4785 to $0.3162 reflecting a lower probability and lower expected payoff in case the option expires in the money. The change of $0.0162 is getting deducted from the call option's delta. However, the put option's delta increases from $-0.5215 to $-0.6838 reflecting a higher probability of the option expiring in the money. Again, the change of $0.0162 is getting deducted from the put option's delta.
Irrespective of the movement in the price of the underlying asset, the option's gamma is positive for a long as highlighted above in the example.
In other words, gamma is always beneficial to a long option.
Practical Applications: An Estimation Tool or A Risk Sensitivity?
'Gamma' sensitivity is important because it helps,
traders understand the potential variability in delta and allows for better hedging strategies, especially during periods of significant price fluctuations.
risk managers as high gamma options pose higher risks due to their sensitivity to even small movements in the underlying price, making them critical to monitor in volatile markets.
Sophisticated Estimation: Black-Scholes-Merton (BSM) Model
As discussed here, traders use the option's delta to predict movements in the option's price based on the movements in the price of the underlying asset.
"delta captures the linear movement and delta changes momentarily"
Mathematically,
If the price of an underlying asset increases (or decreases), the option's delta of both call and put options increases (or decreases) but at a decreasing rate. If it would have been a constant increase or decrease, the question of second-order derivative wouldn't have been in the picture. And this is because of the non-linear relationship between the option's price and the price of the underlying asset as shown below.
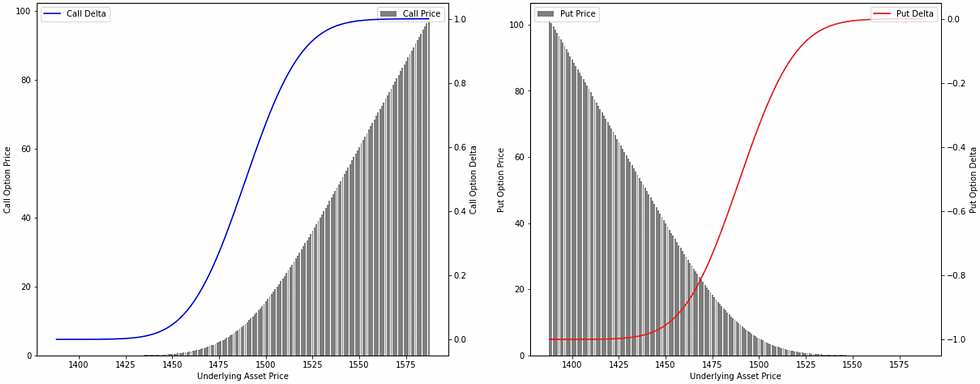
And because of this relationship, the delta curves of both call and put options are not tangent/straight lines as these curves represent that relationship highlighted above.
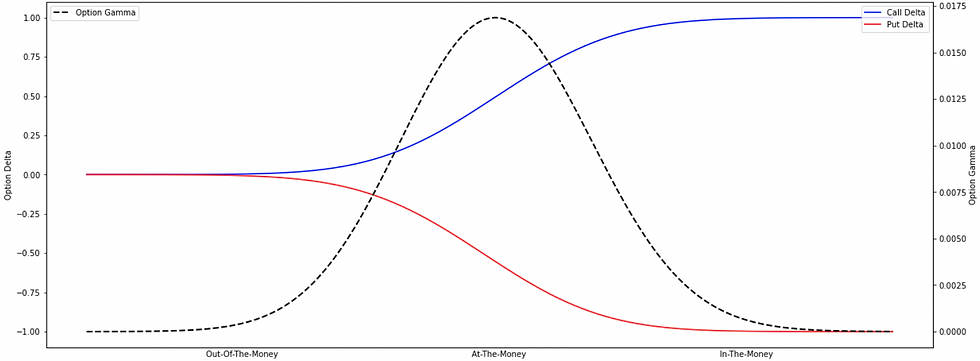
Instead, these curves are seeming to be more like s-shaped and behave differently at different points of moneyness.
for out-of-the-money options: The delta values of both call and put options are almost near 0, a small change in the price of the underlying asset won't be impacting much on the probability, and therefore, the delta value remains reasonably stable resulting in gamma to be almost flat at 0.
for at-the-money options: The delta values of both call and put options are almost 0.5, a small change in the price of the underlying asset will be impacting the delta values to a greater extent as the sensitivity of the option's delta to a change in the price of the underlying asset i.e. option's gamma is highest at this point.
for in-the-money options: The delta values of both call and put options are almost near 1 (absolute-wise), a small change in the price of the underlying asset won't be impacting much on the probability, and therefore, the delta value remains reasonably stable resulting in gamma to be almost flat at 0.
However, it may also change due to the change in the volatility and time-decay, but that is the next topic of our financial book.
The formula that has been stated above with an example is a sensitivity-based formula that strictly goes with explanations 1 and 2. However, professional traders determine the price of an option using some sophisticated models that often resemble the Black-Scholes-Merton (BSM) model. This model provides a mathematical function to estimate the theoretical price of an option by considering market risk factors.
Explanation-3: An option's gamma determines the variability in the expected payoff in case the option expires in the money.
As discussed here, N(d1) is the probability that determines the expected payoff in case the option expires in the money. And,
As per explanation 3, [ St*σ*√T ] determines the variability in the expected payoff in case the option expires in the money.
therefore,
Gamma = [ (LN(St/K) + (r-q+σ^2/2)*T) / σ*√T ] from standard normal distribution / (St*σ*√T)
Example:
[option's delta-gamma series across the spot ladder at a particular strike price]

Using the Black-Scholes equation,
[ (LN(1488.05/1490.00) + (0.06+0.2145^2/2)*0.0055) / 0.2145*√0.0055 ] from standard normal distribution / (1488.05*0.2145*√0.0055)
Gamma = 0.0169
The below table represents options delta-gamma values and prices across the movement in the price of the underlying asset. This can be calculated with the help of the above equation.

Observation 1: Considering an ATM option, the probability of the option landing ITM is 50%, and therefore, the delta value of the call option is near 0.5, a small change in the price of the underlying asset will be impacting the delta values to a greater extent as the sensitivity of the option's delta to a change in the price of the underlying asset i.e. option's gamma is highest at this point.
As the price of the underlying asset increases (from ATM to ITM to deep ITM i.e. from $1488.05 to $1498.05 to $1508.05), the delta of the call option also increases (from 0.4785 to 0.6435 to 0.7843) but at a decreasing rate. As the option gets further ITM, the rate of increase in the option's delta further decreases, and therefore, the sensitivity of the option's delta i.e. option's gamma approaches to 0.
As the price of the underlying asset decreases (from ATM to OTM to deep OTM i.e. from $1488.05 to $1478.05 to $1468.05), the delta of the call option also decreases (from 0.4785 to 0.3162 to 0.1825) but at a decreasing rate. As the option gets further OTM, the rate of increase in the option's delta further decreases, and therefore, the sensitivity of the option's delta i.e. option's gamma approaches to 0.
Observation 2: Considering the other options trading deep ITM or OTM has a greater probability of them getting exercised or lapsed, respectively, as a small change in the price of the underlying asset won't be impacting much on the probability, and therefore, the delta value remains reasonably stable resulting in gamma to be almost flat at 0.

Gamma's Role in Professional Trading
Professional traders are more interested in monitoring option chains and analyzing delta and gamma across multiple strike prices and expiries to evaluate market sentiments and risk exposure.
having both option prices and their corresponding Greeks across strike prices helps them,
estimate any potential change in risk exposures, and identify factors impacting their positions.
adjust their positions by buying or selling options to maintain desired delta exposure or manage directional risks.

Comments