Financial Derivatives And Risk Management: A Practical Interview Guide on Risk Sensitivities (3.0)
- Pankaj Maheshwari

- Aug 25, 2024
- 12 min read
Updated: Sep 29, 2024
Congratulations! You've landed an interview I understand, and now it's time to prepare for it!
One of the most important guides at your disposal is this interview guide. think of it as your roadmap to success, guiding you through the twists and turns of the interview process. Here's how to decode and utilize this essential document effectively.

Start by carefully reading through this interview guide from start to end. Pay attention to any instructions, formatting, or specific questions provided.
Spend time on each topic, take notes, strive for understanding, and, most importantly, attempt to model these complex problems using either Excel or Python.
While this interview guide provides a detailed framework, be prepared to adapt and think on your feet. Interviewers may ask unexpected or follow-up questions to test deeper into certain areas.
After the interview, reflect on your performance and seek feedback from trusted sources, such as mentors, career advisors, or interview coaches. Again, take notes of areas of improvement and incorporate them into your preparation for future interviews.
A Practical Interview Guide on Risk Sensitivities – Delta, Gamma, Vega, Theta, Rho, Volga, Vanna, Duration, DV01, Convexity, CS01
What are the sensitivities to option derivatives?
Option Greeks are risk measures that describe how the price of an option changes in relation to various factors. they are essential for managing and understanding the risks involved in options trading—the most commonly used Greeks are Delta, Gamma, Vega, Volga, Vanna, Theta, and Rho.
Each Greek corresponds to the sensitivity of the option price to a particular variable/risk factor. Understanding them helps traders make informed decisions regarding hedging, risk management, and potential profitability.
Delta is a rate of change in the price of an option with respect to a change in the price of the underlying asset, other factors being constant. In other words, an option's delta is the amount by which the price of an option is expected to change with respect to a $1 change in the price of the underlying asset, other factors being constant.
Mathematically, if the price of an underlying asset increases, the option delta of both call and put options increases too.
The delta of a call option always remains positive (it will range between 0 and 1, representing a positive relationship with the underlying) and the delta of a put option always remains negative (ranging between -1 to 0, representing a negative relationship with the underlying).
'Delta' sensitivity is important because it helps, (1). traders estimating the movement in the price of an option for any change in the price of the underlying asset. (2). risk managers to gauge the directional risk and being the most crucial risk attribute for analysis though it explains the first-order risk only.
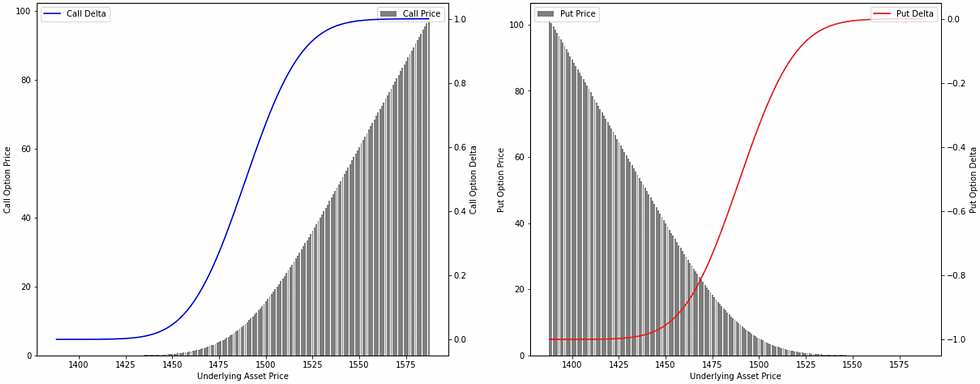
Delta for Call Options: Delta for a call option ranges between 0 and 1. If a call option has a delta of 0.5, a $1 increase in the underlying price of the asset would result in a $0.50 increase in the price of the call option.
Delta for Put Options: Delta for a put option ranges between -1 and 0. A put option with a delta of -0.5 would decrease by $0.50 for every $1 increase in the price of the underlying asset.
there is a true relationship between the delta of a call option and the delta of a put option! It is observed that the sum of absolute values of the delta of a call and a put is equal to 1. This relation is prevailing due to the Put-Call Parity theory which states that a protective put is equivalent to a fiduciary call, and therefore, a combination of a long call and a short put is equivalent to a long forward whose delta is close to 1.
Put Delta = Call Delta - 1
for example, If the delta of a call option is 0.5620, the delta of a put option is 0.5620 - 1 = -0.4380. It means, that if the price of the underlying asset increases by $1, the price of a call option is expected to increase by $0.5620 and that of a put option to decrease by $0.4380. Simple right? -- not actually!
this relationship will hold good only if the underlying is a non-dividend or non-coupon-paying asset.
❗Be prepared to explain how would you use Delta to assess the risk of a portfolio, prepare an example of how you would manage an options position considering both Delta and Charm as expiration approaches, and how would you adjust Delta in response to significant price movements in the underlying asset.
Gamma is a rate of change in the option's delta with respect to a change in the price of the underlying asset, other factors being constant. In other words, an option's gamma is an amount by which the option's delta is expected to change with respect to a $1 change in the price of the underlying asset, other factors being constant.
Gamma influences the delta of calls and puts in the same direction and gamma is always positive for long and negative for short.
'Gamma' sensitivity is important because it helps, (1). traders to estimate the movement in the option's delta for any change in the price of the underlying asset. (2). risk managers to gauge the directional risk add-on to the first-order risk and is the most crucial risk attribute for analysis as it explains the second-order risk, sometimes referred to as higher-order risk.
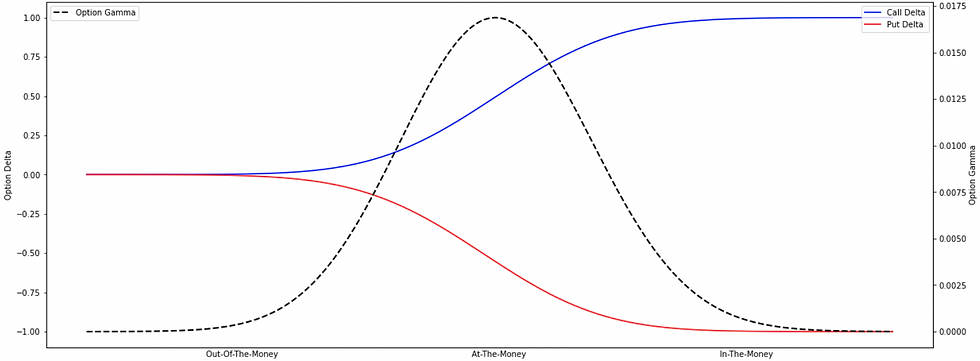
𝘋𝘦𝘭𝘵𝘢 𝘮𝘦𝘢𝘴𝘶𝘳𝘦𝘴 𝘵𝘩𝘦 𝘰𝘱𝘵𝘪𝘰𝘯'𝘴 𝘴𝘦𝘯𝘴𝘪𝘵𝘪𝘷𝘪𝘵𝘺 𝘵𝘰 𝘤𝘩𝘢𝘯𝘨𝘦𝘴 𝘪𝘯 𝘵𝘩𝘦 𝘶𝘯𝘥𝘦𝘳𝘭𝘺𝘪𝘯𝘨 𝘢𝘴𝘴𝘦𝘵'𝘴 𝘱𝘳𝘪𝘤𝘦, 𝘸𝘩𝘪𝘭𝘦 𝘨𝘢𝘮𝘮𝘢 𝘮𝘦𝘢𝘴𝘶𝘳𝘦𝘴 𝘵𝘩𝘦 𝘳𝘢𝘵𝘦 𝘢𝘵 𝘸𝘩𝘪𝘤𝘩 𝘥𝘦𝘭𝘵𝘢 𝘤𝘩𝘢𝘯𝘨𝘦𝘴 𝘪𝘯 𝘳𝘦𝘴𝘱𝘰𝘯𝘴𝘦 𝘵𝘰 𝘤𝘩𝘢𝘯𝘨𝘦𝘴 𝘪𝘯 𝘵𝘩𝘦 𝘶𝘯𝘥𝘦𝘳𝘭𝘺𝘪𝘯𝘨 𝘢𝘴𝘴𝘦𝘵'𝘴 𝘱𝘳𝘪𝘤𝘦. 𝘈 𝘩𝘪𝘨𝘩 𝘎𝘢𝘮𝘮𝘢 𝘪𝘮𝘱𝘭𝘪𝘦𝘴 𝘵𝘩𝘢𝘵 𝘋𝘦𝘭𝘵𝘢 𝘤𝘢𝘯 𝘤𝘩𝘢𝘯𝘨𝘦 𝘲𝘶𝘪𝘤𝘬𝘭𝘺, 𝘮𝘦𝘢𝘯𝘪𝘯𝘨 𝘵𝘩𝘦 𝘰𝘱𝘵𝘪𝘰𝘯 𝘣𝘦𝘤𝘰𝘮𝘦𝘴 𝘮𝘰𝘳𝘦 𝘴𝘦𝘯𝘴𝘪𝘵𝘪𝘷𝘦 𝘵𝘰 𝘱𝘳𝘪𝘤𝘦 𝘮𝘰𝘷𝘦𝘮𝘦𝘯𝘵𝘴 𝘪𝘯 𝘵𝘩𝘦 𝘶𝘯𝘥𝘦𝘳𝘭𝘺𝘪𝘯𝘨 𝘢𝘴𝘴𝘦𝘵.
Option's gamma is a second-order derivative "a derivative (gamma) of a derivative (delta)" as it measures the rate of change of an option's delta stating how fast an option changes its directional movement.
It measures how much delta changes when the underlying asset's price changes. Since gamma is a second-order derivative, it is always positive for both long calls and long puts, meaning that the delta becomes more sensitive as the underlying price moves.
for the ATM options, the probability of the option landing ITM (In-The-Money) is close to 50%, and therefore, the delta value of the call option is near 0.5. A small change in the price of the underlying asset will significantly impact the delta, as the option's gamma, which measures the sensitivity of delta to changes in the underlying price, is highest at this point.
for deep ITM or OTM options, the probability of the option being exercised (for ITM) or expiring worthless (for OTM) is high, and a small change in the price of the underlying asset does not significantly affect this probability. As a result, the delta value remains relatively stable, and the gamma approaches zero, indicating low sensitivity of delta to changes in the underlying price.
❗You may be asked how you would manage a portfolio where Gamma is increasing for short-dated or ATM options.
Understanding Vega: A Deep Dive into Options Greek
Vega is a rate of change in the price of an option with respect to a change in the volatility of the underlying asset, other factors being constant. In other words, an option's vega is an amount by which the price of an option is expected to change with respect to a 1% change in the volatility of the underlying asset, other factors being constant.
If the volatility of the underlying asset increases, the vega of both call and put options increases too.
It is important because it helps traders and risk managers to estimate the potential impact of changes in volatility on an option's price. Vega is typically represented as a positive number.
Vega tells you how much the option’s price will increase or decrease with a 1% move in implied volatility. for example, if an option has a Vega of 0.20, and the implied volatility increases by 1%, the option’s price will increase by $0.20.
This is particularly important for ATM options, as they tend to have the highest Vega, making them more sensitive to changes in volatility compared to deep ITM or OTM options.
ATM options generally have the highest Vega because changes in volatility have a significant impact on whether they will expire ITM or not.
Deep ITM or OTM options have lower Vega because volatility plays a lesser role in determining their final outcome.
Vega is highest for longer-dated options. As expiration approaches, the option becomes less sensitive to volatility changes, and Vega decreases.
For short-term options, changes in volatility have a more limited impact, as time decay (Theta) dominates.
Assume that a portfolio holds ATM call options with a Vega of 0.50. If the implied volatility of the underlying asset increases by 2%, the option price will increase by 0.50 (Vega) × 2 (Implied Vol Change) = $1.
𝘐𝘯 𝘷𝘰𝘭𝘢𝘵𝘪𝘭𝘦 𝘮𝘢𝘳𝘬𝘦𝘵 𝘤𝘰𝘯𝘥𝘪𝘵𝘪𝘰𝘯𝘴, 𝘵𝘩𝘦 𝘱𝘰𝘳𝘵𝘧𝘰𝘭𝘪𝘰 𝘮𝘢𝘯𝘢𝘨𝘦𝘳 𝘸𝘰𝘶𝘭𝘥 𝘢𝘴𝘴𝘦𝘴𝘴 𝘸𝘩𝘦𝘵𝘩𝘦𝘳 𝘵𝘩𝘪𝘴 𝘪𝘯𝘤𝘳𝘦𝘢𝘴𝘦𝘥 𝘦𝘹𝘱𝘰𝘴𝘶𝘳𝘦 𝘢𝘭𝘪𝘨𝘯𝘴 𝘸𝘪𝘵𝘩 𝘵𝘩𝘦𝘪𝘳 𝘳𝘪𝘴𝘬 𝘢𝘱𝘱𝘦𝘵𝘪𝘵𝘦 𝘰𝘳 𝘪𝘧 𝘵𝘩𝘦𝘺 𝘯𝘦𝘦𝘥 𝘵𝘰 𝘩𝘦𝘥𝘨𝘦 𝘵𝘩𝘦 𝘱𝘰𝘴𝘪𝘵𝘪𝘰𝘯.
Traders and Risk managers must understand Vega to hedge portfolios effectively, especially in environments with volatile market conditions.
💡Traders often maintain a Vega-neutral position, which means their portfolio's overall Vega is close to zero. This protects them from volatility shocks. If the market’s implied volatility unexpectedly increases or decreases, the portfolio's value remains stable.
💡In periods of expected high volatility, Vega becomes crucial. A trader holding high Vega options may profit from increased volatility, while low Vega options may offer more stability in quieter markets.
❗Prepare for questions about how to adjust your portfolio if volatility spikes and your Vega exposure increases significantly.
Understanding Theta: A Deep Dive into Options Greek
Theta is a rate of change in the price of an option with respect to a change in the time remaining until expiration, other factors being constant. In other words, an option's theta is an amount by which the price of an option is expected to change with respect to a one-day decrease in the time remaining until expiration, other factors being constant.
Theta is negative for both call and put options because time decay works against the option holder. The closer an option gets to expiration, the faster its value erodes.
Theta is highest for ATM options, as they are the most sensitive to time decay. Deep ITM or OTM options have lower Theta because their intrinsic value is less affected by the passage of time.
𝘛𝘩𝘦𝘵𝘢 𝘪𝘴 𝘤𝘳𝘶𝘤𝘪𝘢𝘭 𝘧𝘰𝘳 𝘵𝘪𝘮𝘦-𝘴𝘦𝘯𝘴𝘪𝘵𝘪𝘷𝘦 𝘴𝘵𝘳𝘢𝘵𝘦𝘨𝘪𝘦𝘴. 𝘐𝘧 𝘺𝘰𝘶 𝘩𝘰𝘭𝘥 𝘭𝘰𝘯𝘨 𝘰𝘱𝘵𝘪𝘰𝘯𝘴, 𝘵𝘪𝘮𝘦 𝘥𝘦𝘤𝘢𝘺 𝘸𝘰𝘳𝘬𝘴 𝘢𝘨𝘢𝘪𝘯𝘴𝘵 𝘺𝘰𝘶, 𝘮𝘦𝘢𝘯𝘪𝘯𝘨 𝘺𝘰𝘶 𝘭𝘰𝘴𝘦 𝘷𝘢𝘭𝘶𝘦 𝘦𝘢𝘤𝘩 𝘥𝘢𝘺. 𝘖𝘯 𝘵𝘩𝘦 𝘰𝘵𝘩𝘦𝘳 𝘩𝘢𝘯𝘥, 𝘪𝘧 𝘺𝘰𝘶 𝘢𝘳𝘦 𝘴𝘩𝘰𝘳𝘵 𝘰𝘱𝘵𝘪𝘰𝘯𝘴, 𝘵𝘪𝘮𝘦 𝘥𝘦𝘤𝘢𝘺 𝘸𝘰𝘳𝘬𝘴 𝘪𝘯 𝘺𝘰𝘶𝘳 𝘧𝘢𝘷𝘰𝘳 𝘢𝘴 𝘺𝘰𝘶 𝘨𝘢𝘪𝘯 𝘧𝘳𝘰𝘮 𝘵𝘩𝘦 𝘦𝘳𝘰𝘴𝘪𝘰𝘯 𝘰𝘧 𝘵𝘩𝘦 𝘰𝘱𝘵𝘪𝘰𝘯'𝘴 𝘷𝘢𝘭𝘶𝘦.
Near Expiration: the impact of Theta accelerates as expiration approaches. Traders must carefully manage their positions when time decay is at its peak to avoid large losses.
Short vs. Long-Dated Options: short-dated options have a much higher Theta than long-dated options. A trader holding a short-dated option close to expiration will see its value decay much faster than an option with several months left until expiration.
for example, consider an ATM option with a Theta of -0.05, meaning that with each passing day, the option will lose $0.05 in value due to time decay. Over the course of 5 days, the option’s price will drop by approximately $0.25, assuming no other factor changes.
An options desk or a portfolio with high Theta, time decay needs to be managed. If the options are not expected to move ITM soon, traders might have to close or adjust their positions to avoid further loss.
💡shorting options can be a strategy to take advantage of time decay, but it comes with risks if the underlying price moves unexpectedly.
Whether you're trading short or long-dated options, understanding how time affects your positions can make the difference between profit and loss.
❗You may be asked to calculate how Theta impacts a long straddle if volatility stays low, and what strategies can mitigate it.
Understanding Rho: A Deep Dive into Options Greek
Rho is a rate of change in the price of an option with respect to a change in the interest rates, other factors being constant. In other words, an option's rho is the amount by which the price of an option is expected to change with respect to a 1% change in interest rates, other factors being constant.
If the interest rates increase, the rho of both call and put options increase for long positions and decrease for short positions.
Rho is typically represented as a positive or negative number, depending on whether the option is a call or put and whether it is long or short.
It is important because it helps traders and risk managers estimate the potential impact of changes in interest rates on an option's price.
Given that the delta of a call option is 0.5620, what would be the delta of a corresponding put option?
(assuming that the underlying asset is a: dividend-paying stock, non-dividend-paying stock.)
The delta of a put option is related to the delta of a call option by the formula:
delta of a put option = delta of a call option - 1
for example,
If the underlying asset is a non-dividend-paying stock and the delta of the call option is 0.5620, the delta of the corresponding put option can be calculated as follows:
Delta of Put Option = 0.5620 - 1 = -0.4380
this means that if the price of the underlying non-dividend-paying stock increases by $1, the price of the call option is expected to increase by $0.5620, while the price of the put option is expected to decrease by $0.4380
(this relationship will hold good only if the underlying is a non-dividend or non-coupon-paying asset.)
for a dividend-paying stock, the delta relationship becomes more complex due to the impact of dividends on the pricing of options. While the exact delta of the put option in this case would generally be less negative than in the non-dividend-paying case, the basic relationship of:
delta of a put option = delta of a call option - 1
still holds in principle. However, it's important to note that dividends decrease the value of call options and increase the value of put options, meaning the delta of the call option might be slightly lower, and thus the delta of the put option might be slightly less negative.
How does the delta of an option behave with respect to moneyness?
And what are the implications of this behavior for different types of options (ATM, ITM, OTM)?
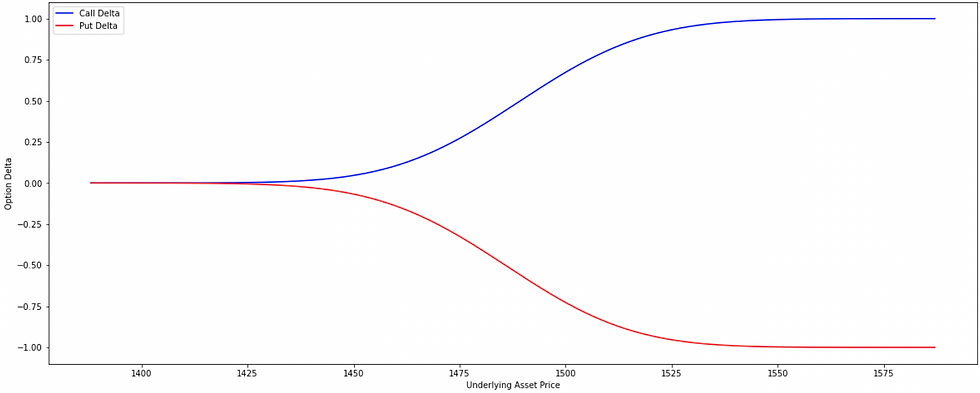
the delta of an option reflects the sensitivity of the option's price to changes in the price of the underlying asset. The behavior of delta varies significantly depending on the moneyness of the option, which refers to whether the option is at-the-money (ATM), in-the-money (ITM), or out-of-the-money (OTM).
Delta Behavior for ATM Options: ATM Options are those where the price of the underlying asset is very close to the strike price. The delta of an ATM call option is close to 0.5, meaning there's approximately a 50% probability that the option will end up in-the-money (ITM) at expiration. Similarly, the delta of an ATM put option is around -0.5. This 50/50 probability is because the underlying asset has equal chances of moving either above or below the strike price. Therefore, the delta for ATM options tends to be around 0.5 for calls and -0.5 for puts.
Delta Behavior for ITM and Deep ITM Options: ITM Options are where the underlying asset’s price is above the strike price for calls or below the strike price for puts. As the underlying asset price increases and the option becomes ITM or deep ITM, the delta of a call option increases (from 0.55 at ATM to 0.65 ITM to 0.75 deep ITM).
As the option moves further ITM, the probability that it will be exercised increases, leading to a higher delta, the delta approaches 1 for calls (and -1 for puts), indicating a near certainty of being exercised.
This makes deep ITM options more attractive, as their value will closely mirror movements in the underlying asset.
Delta Behavior for OTM and Deep OTM Options: OTM Options are where the underlying asset’s price is below the strike price for calls or above the strike price for puts. As the underlying asset price decreases and the option becomes OTM or deep OTM, the delta of a call option decreases (from 0.45 at ATM to 0.35 OTM to 0.25 deep OTM).
As the option moves further OTM, the probability that it will be exercised decreases, leading to a lower delta, the delta approaches 0 for calls (and 0 for puts), indicating a low likelihood of being exercised.
This lower probability makes deep OTM options less attractive as their value is less responsive to changes in the underlying asset.
What's the difference between discrete and continuous stochastic processes?
Stochastic processes are mathematical models used to describe systems that evolve over time with some degree of randomness. They can be broadly classified into several categories based on their characteristics.
Discrete-Time vs. Continuous-Time Stochastic Processes:
Discrete-Time Stochastic Processes: These processes are defined at specific intervals, meaning that changes to the process can only occur at these fixed time points. For instance, if we look at daily stock prices, where the price is recorded at the end of each trading day, this forms a discrete-time process. Mathematically, we model these processes using sequences of random variables, such as Xt, where t represents discrete time steps.
Continuous-Time Stochastic Processes: In these processes, the system can change at any point in time. For example, stock prices that fluctuate continuously throughout the trading day are modeled as continuous-time processes. These are often represented using stochastic differential equations (SDEs), such as those in the Black-Scholes model used for option pricing.
Continuous-Variable vs. Discrete-Variable Stochastic Processes:
Continuous-Variable Stochastic Processes: These processes involve variables that can take any value within a certain range. An example is the measurement of temperature, which can vary continuously within a range. Such processes are modeled using probability density functions, like the normal distribution.
Discrete-Variable Stochastic Processes: Here, the variable can only take on certain distinct values. For instance, the number of arrivals at a service center in a given time frame is a discrete variable process, where the number of arrivals can be 0, 1, 2, and so on. This is often modeled using probability mass functions, such as the binomial distribution.
Understanding these classifications helps in selecting appropriate models for analyzing different types of random phenomena. For instance, in financial applications, continuous-time stochastic processes like Brownian motion are crucial for modeling asset prices and risk, while discrete-time models might be used for analyzing monthly returns.

Comentarios